Quantum-Accelerated Stabilization for Markov-Chain Averaging
A band–window stabilization criterion with quadratic quantum speedup — J. Landers
Introduction & Context
We estimate an aggregate $\mu=\mathbb{E}_\pi[f]$ over a finite state space $S$ with target distribution $\pi$ and bounded observable $f:S\to[a,b]$. When i.i.d. sampling from $\pi$ is unavailable, we employ a reversible Markov chain with transition matrix $P$ and stationary distribution $\pi$ (i.e. $\pi P=\pi$), drawing a trajectory $(X_t)_{t\ge1}$ and forming the running mean
Classical baseline
Mixing time. Up to logarithmic factors, the mixing time satisfies $\tau_{\text{mix}}\asymp 1/\gamma$. Classical MCMC estimation of $\mu$ to additive error $\varepsilon$ with constant success probability requires
Stabilization via band & window
Fix tolerance $\delta>0$ and window length $W\in\mathbb{N}$. For a sequence of estimates $(m_t)_{t\ge1}$, define the stabilization start time
Interpretation: once the estimate enters the band $[\mu-\delta,\mu+\delta]$ and remains for $W$ successive steps, the flow is declared stabilized.
Quantum primitives
Assume a Szegedy-type quantum walk for $P$ and an implementation of $f$ suitable for amplitude estimation (AE). A single quantum mean-estimation call outputs $m$ with
using oracle time
Our contributions at a glance
We use the band–window lens to express quantum advantage operationally. Two theorems capture complementary goals:
-
Theorem 1 (First-window guarantee).
If you want stabilization immediately, run $W$ independent AE calls with per-call
failure tuned to $\alpha\!\le\!\beta/W$. With probability $\ge 1-\beta$, all $W$ estimates
already lie within $[\mu-\delta,\mu+\delta]$, so $t^\star(\delta,W)\le 1$. The total time is
$$T_{\mathrm{q,stab}}(\delta,W,\beta)=\tilde O\!\left(\frac{\sqrt{\tau_{\text{mix}}}}{\delta}\,W\,\log\tfrac{W}{\beta}\right),$$compared to the classical$$T_{\mathrm{cl,stab}}(\delta,W)=\tilde O\!\left(\frac{\tau_{\text{mix}}}{\delta^2}\,W\right).$$Plain English: pay the cost up front so the very first window of length $W$ is already good.
-
Theorem 2 (Anytime, persistent guarantee).
Run AE sequentially with a growing-precision schedule and a careful failure-allocation across
rounds. With probability $\ge 1-\beta$, the process eventually enters a stabilization
window of length $W$ and, upon entry, that window persists for the full $W$ steps. The query
complexity scales as
$$\tilde{O}\!\left(\frac{1}{\delta}\,\log\frac{W}{\beta}\right),$$showing the same quadratic-in-$1/\delta$ improvement over the classical analogue while providing a uniform-in-time (anytime) certification. Plain English: you don’t fix the time in advance; whenever a valid window first appears, you can certify it will stick for $W$ steps.
Main Theorem (Quantum band–window stabilization)
Given: $\delta>0$, $W\in\mathbb{N}$, and failure budget $\beta\in(0,1)$. Run $W$ independent AE calls producing $m_1,\dots,m_W$ with per-call failure $\alpha\le\beta/W$. Then
so $t^\star(\delta,W)\le1$ with probability at least $1-\beta$. The total quantum time is
Sketch. Boost each AE call to failure $\alpha$ by standard repetition/median, incurring a $\log(1/\alpha)$ factor. Independence yields $(1-\alpha)^W\ge1-\beta$ when $\alpha\le\beta/W$, implying the first window lies in-band with probability $\ge1-\beta$. Multiplying per-call time by $W$ gives the bound. $\square$
Classical comparison
To achieve the same stabilization classically with $W$ simultaneous $\delta$-accurate estimates (e.g. independent blocks), one needs
Takeaway
The band–window stabilization lens yields a simple, operational statement of quantum advantage: with probability $1-\beta$, stabilization occurs in the very first window under quantum AE, with total time
compared to the classical
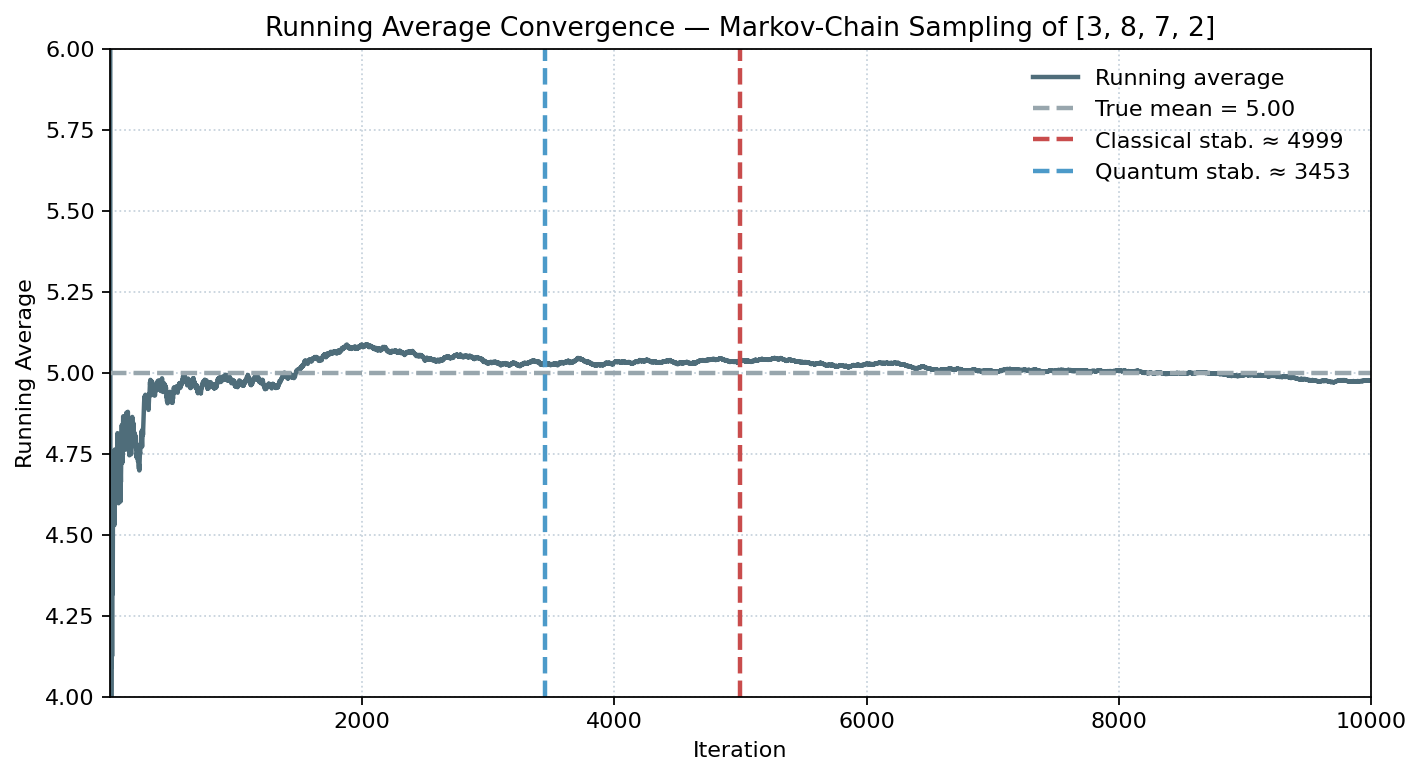
Simulation Example: Running Average Convergence
To illustrate the stabilization phenomenon, we simulate a 10,000-step run of the
uniform “teleporting” Markov chain over the list [3, 8, 7, 2]. The plot
shows the running average (solid line) converging toward the true mean (dashed line).
Vertical dashed lines mark the expected stabilization times under the
classical and quantum bounds.
Remarks and Stabilization Retention
Theorem 1 established a resource bound for achieving a stabilization window at a fixed horizon, essentially asking how many queries are needed so that $W$ consecutive estimates fall inside the target band with high probability. In many settings, however, one desires a stronger anytime guarantee: we do not fix the horizon in advance, but instead run the estimator until it naturally stabilizes, and then ask for assurances that once a window appears it truly reflects convergence.
The following theorem formulates this idea. By coupling an iterative amplitude-estimation schedule with a careful allocation of failure probability across rounds, we obtain stabilization that is valid uniformly over time. This reframes the problem: rather than bounding error at a single time, we bound the complexity of entering and retaining a valid window whenever it first occurs.
Theorem 2 (Windowed Quantum AE: Anytime Stabilization Guarantee)
Let $f:S\to[0,1]$ with mean $\mu=\mathbb{E}_\pi[f]$. An iterative amplitude estimation (AE) procedure produces sequential estimates $\hat\mu_{1},\hat\mu_{2},\ldots$. Define stabilization as $W$ consecutive outputs all lying in $[\mu-\delta,\mu+\delta]$.
There exists a schedule of AE calls such that, with probability at least $1-\beta$, the process eventually enters such a stabilization window and it persists for the full $W$ steps. The total query complexity is
$$\tilde{O}\!\left(\frac{1}{\delta}\,\log\frac{W}{\beta}\right).$$
Simulation Example: Certified Stabilization (Theorem 2)
We run the same 10,000-step simulation of the uniform “teleporting” Markov chain over
[3, 8, 7, 2] and visualize the certified stabilization guarantee.
The left panel shows the running average (solid line) with a shaded stabilization band
around the true mean (dashed line) using δ = 0.1. We then detect
the first window of length W = 500 where the trajectory remains entirely
within the band and highlight that window in maroon. This illustrates the
Theorem 2 notion of persistence (staying in-band for W steps),
which is stronger than the “first entry” view from Theorem 1.
The right panel compares the calculated certification runtimes to detect and certify
such a window at confidence 1 − β (here β = 0.05):
the classical detector scales like (1/δ²)·log(W/β), while the quantum
WQAE detector scales like (1/δ)·log(W/β), showing the quadratic savings
in 1/δ for the quantum procedure (same color scheme as elsewhere).
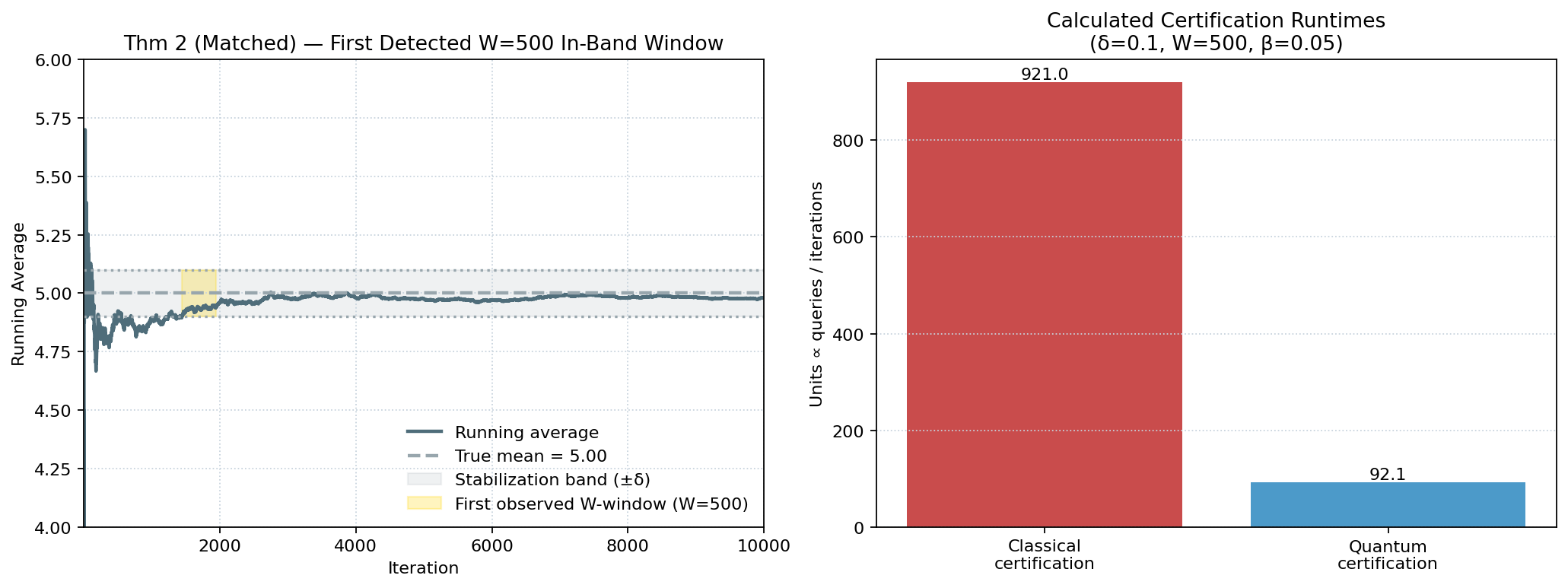
W=500 in-band window highlighted in maroon. Right—calculated certification
runtimes showing classical (1/δ²)·log(W/β) vs. quantum
(1/δ)·log(W/β) scaling (with identical W, δ, β).
Conclusion
The band–window viewpoint turns mean estimation into a simple operational goal: enter the
calm zone around μ and stay there long enough to trust it. Quantum amplitude
estimation makes that goal immediate, certifying the very first window with a quadratic
saving in 1/δ. The anytime schedule upgrades “first entry” into persistent,
uniform-in-time stabilization. The simulations echo this story visually: a clear band,
a highlighted window, and parallel runtime scalings that differ only in their dependence
on accuracy. In practice, this suggests using stabilization windows as drop-in, model-agnostic
stopping rules, with natural extensions to adaptive bands, heterogeneous windows, and
non-reversible chains left as pragmatic next steps.